Vlnění a optika (přednáška)
Přednáška pro přípravný kurs fyziky
– viz http://cs.wikiversity.org/wiki/MedFyz
Vzhled:
- chick (úprava skinu pro přednášku – viz User:Kychot/chick.css)
- monobook běžný vzhled
Příklady - modelové otázky pro:
- 1. LF UK (Vítek, Rakovič 2007) č. 1064 – 1186
- 2. LF UK (Amler et al, 4. vyd. 2009) č. 706 – 853
Vlnění II.
[editovat]Následující jevy platí pro různé druhy vlnění:
Difrakce
[editovat]= "ohyb vlnění"
- Huygensův princip
- koherentní vlny (konstantní fázový rozdíl)
- interference vlnění
Difrakci pozorujeme při interakci vlnění s nějakou překážkou.
Čím delší je vlna ve srovnání s rozměry překážky, tím zřetelnější jsou difrakční jevy.
V obvyklém životě:
- λsvětla cca 390–740 nm < předměty ⇒ světlo se šíří téměř přímočaře, předměty vrhají stíny
- λ zvuku ∼ předměty ⇒ zvuk se ohýbá za překážky;
(např. tón c' = 262 Hz, λ = 340/262 ≐ 1,3 m)
hory – je to jinak - rádiové vlny:
- střední vlny – např. 1 MHz, λ = 3.108/106 = 300 m
- VKV – např. 100 MHz, λ = 3.108/108 = 3 m
- gigahertzové vlny – např. 3 GHz, λ = 3.108/3.109 = 10 cm

Difrakce:
- na štěrbině – Fraunhofferova difrakce (ohyb rovinné vlny)
- stín za předmětem
- na hraně
- na mřížce
-
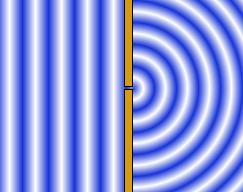
Úzká štěrbina – Huygensův princip
-
Střední štěrbina
-
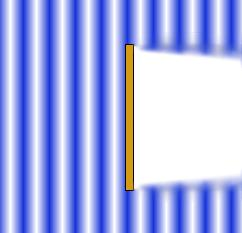
Široká štěrbina – vlivem interference se zmenšuje ohyb
-
Úhel šíření vlny za štěrbinou
-
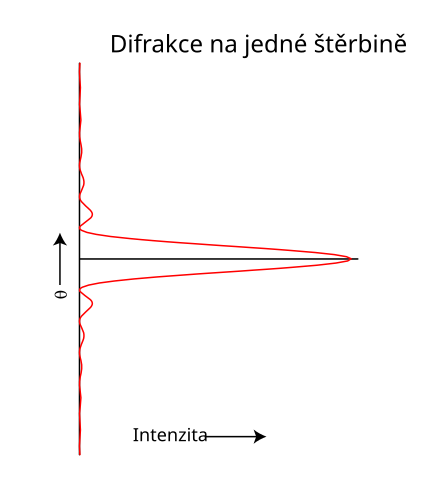
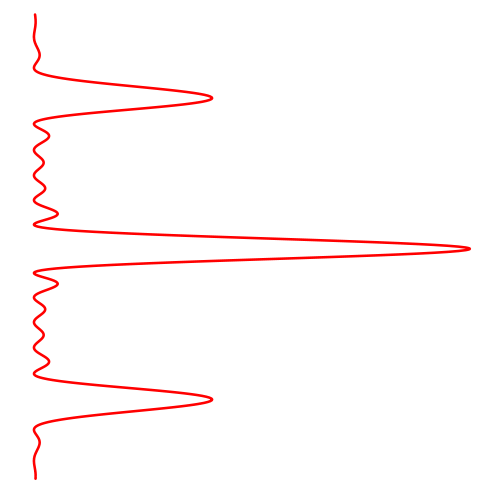
Graf rozložení intenzity v závislosti na úhlu šíření vlny
-
Stín za velkou překážkou
Dvouštěrbinový experiment
[editovat]
-
Youngův náčrtek, kde prezentuje svůj experiment Královské společnosti r. 1803.
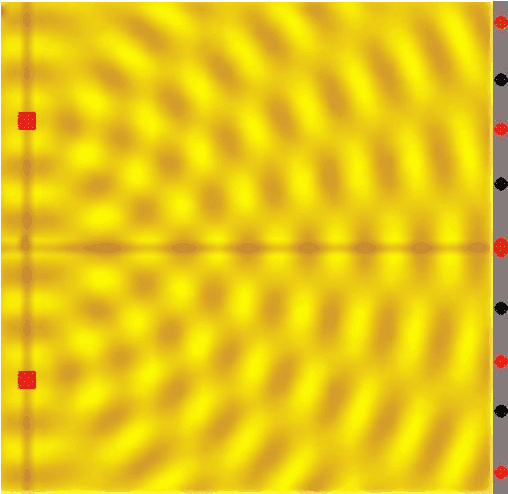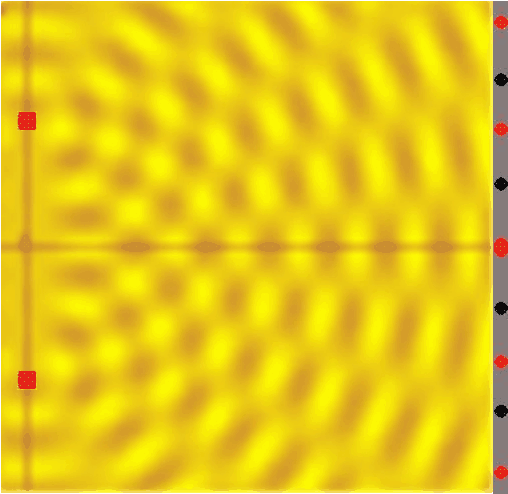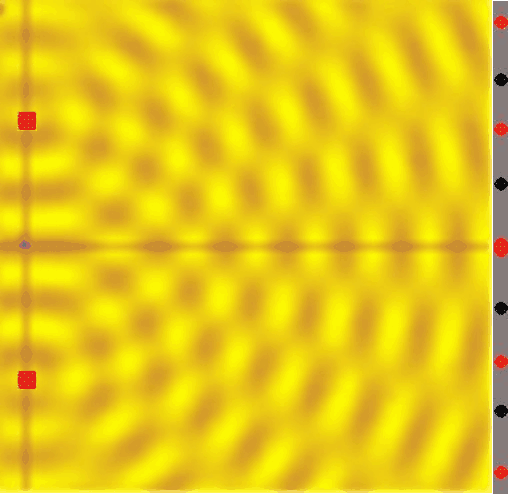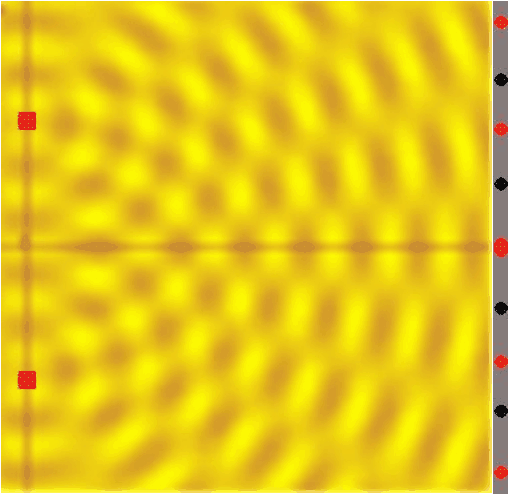
-
Schema dvouštěrbinového experimentu
Podmínka maxima:
dráhový rozdíl Δ = d . sin(α) = k . λ
⇒ pro různé λ jsou maxima na různých místech
⇒ rozklad bílého světla na spektrální barvy
Optická mřížka
[editovat]-
Difrakce na optické mřížce
Difrakce na krystalech
[editovat]-
Difrakce na krystalové mřížce
Odraz vlnění
[editovat]- úhel odrazu α' = úhel dopadu α
- ⇐ dráhový rozdíl = 0
- ⇒ pouze v tomto případě se vlny při interferencí neruší
Lom vlnění
[editovat]-
lom vlnění
Snellův zákon:
sin(α)/sin(β) = c1/c2
Vidíme, že směr šíření vlny je kolmý na vlnoplochu.
Světlo
[editovat]- elektromagnetické vlnění
- příčné vlnění – dva navzájem kolmé vektory a oba kolmé na směr šíření:
- vektor intenzity elektrického pole E
- vektor magnetické indukce B
- šíří se i ve vakuu (dokonce nejrychleji)
- dualismus: vlna i částice (fotony)
Označujeme tak pouze viditelnou část elektromagnetického spektra:
- 390 nm = fialový konec (krátké λ)
- 740 nm = červený konec (dlouhé λ)
Fyzikální vlastnosti ovšem překračují hranice lidských smyslů:
- UV < 390 nm
- IR > 740 nm
Rychlost šíření světla
[editovat]Nejrychlejší ve vakuu:
fázová rychlost c0 ≐ 3.108 [m/s]
Ve všech jiných látkách pomalejší:
c = c0/n
absolutní index lomu n > 1
λ = c/f ⇒
λ1/λ2 = c1/c2 = n2/n1
| prostředí | n |
|---|---|
| vakuum | 1 |
| vzduch | 1,0003 |
| led | 1,31 |
| voda | 1,33 |
| sklo | 1,5 až 1,9 |
| Chlorid sodný | 1,52 |
| vápenec | řádný 1.6–1.4, mimořádný 1.9–1.5 |
| diamant | 2,42 |
Snellův zákon:
sin(α)/sin(β) = c1/c2 = n2/n1 = relativní index lomu
Fermatův princip
[editovat]Světlo se v prostoru šíří z jednoho bodu do druhého po takové dráze, aby doba potřebná k proběhnutí této dráhy byla co nejkratší.
(Moderní formulace: stacionární)
Disperse světla
[editovat]n = n(f) ... rostoucí fce
n = n(λ) ... klesající fce
⇒ světla různých vlnových délek, různých frekvencí, různých barev se šíří látkovým prostředím jinak rychle
⇒ různě se lámou:
Hranol
[editovat]-
Lom světla hranolem
Duha
[editovat]
Spektroskop
[editovat]- mřížkový
- hranolový
-
Freaunhofer demonstruje spektroskop
Geometrická (paprsková) optika
[editovat]- čočka
- spojná = spojka
- rozptylná = rozptylka
- zrcadlo
- rovinné
- vyduté
- vypuklé
- dalekohled
- mikroskop
Čočky
[editovat]Spojka
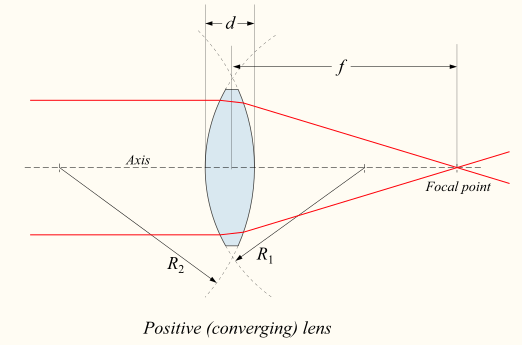
[editovat]Průchod vln spojkou
[editovat]Ohnisko spojky
[editovat]Oko a fotoaparát
[editovat]Zobrazení vzdáleného předmětu jako skutečného převráceného obrazu:
Znaménková konvence
[editovat]V tomto případě jsou všechny vzdálenosti kladné, jen velikost obrazu je záporná (protože je převrácený).
Rovnice čočky
[editovat]
Někdy se vzdálenost předmětu označuje a a vzdálenost obrazu a'
Zobrazení celého předmětu
[editovat]a zvětšení či zmenšení obrazu
[editovat]
Zvětšení Z = velikost obrazu / velikost předmětu = y' / y = -a' / a
Princip lupy
[editovat]Zobrazení blízkého předmětu jako zdánlivého vzpřímeného obrazu:
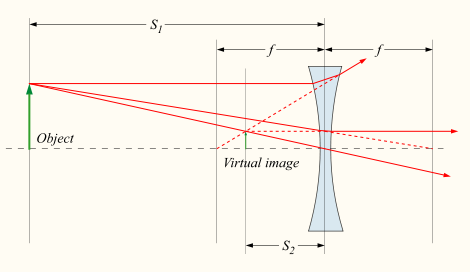
Rozptylka
[editovat]Zobrazení předmětu jako zdánlivého vzpřímeného obrazu:
Vady čoček
[editovat]Sférická vada
[editovat]Barevná vada
[editovat]Astigmatismus
[editovat]Oko
[editovat]René Descartes (1596-1650): L’homme de René Descartes, et la formation du foetus…. Paris: Compagnie des Libraires, 1729. (prvně publikováno 1677)
Akomodace
[editovat]Snížení akomodační schopnosti ve stáří = presbyopie
Refrakční vady
[editovat]Myopie = krátkozrakost
[editovat]Hypermetropie = dalekozrakost
[editovat]
Zrcadlo
[editovat]Rovinné
[editovat]Zdánlivý obraz, zdcadlově převrácený:
Zdcadlová symetrie, chiralita: např. levotočivá spirála se zobrazí jako pravotočivá – podobná synmetrie existuje např. u některých chemických sloučenin.
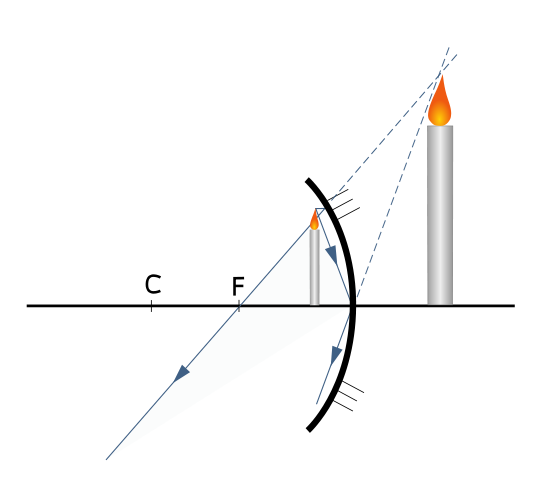
Konkávní = vyduté
[editovat]lat. cavum, cavus = dutina, cavus = dutý, con-cavus = vyhloubený
Pracuje podobně jako spojka:
neboť f = R/2
Konvexní = vypuklé
[editovat]lat. convexus = klenutý
Optické přístroje
[editovat]Dalekohledy
[editovat]reflektory
[editovat]Newtonův
[editovat]refraktory
[editovat]Keplerův
[editovat]Zvětšení Z = f1 / f2
Galileův = holandský
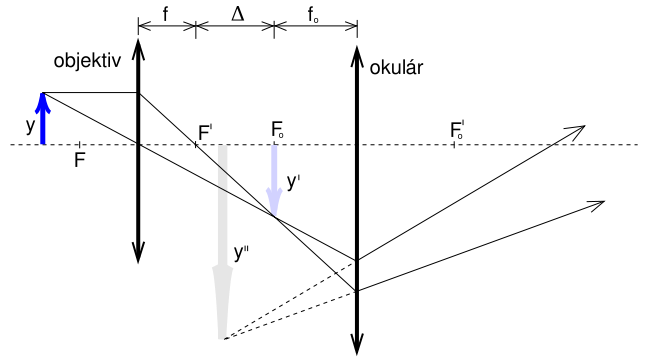
[editovat]Mikroskop
[editovat]Lineární zvětšení mikroskopu:
- a označuje zvětšení objektivu a okuláru
- je obrazová ohnisková vzdálenost objektivu
- je předmětová ohnisková vzdálenost okuláru
- je optický interval mikroskopu
- je konvenční zraková vzdálenost.